Hopping to Numbers

Tag: symplectic-matrices

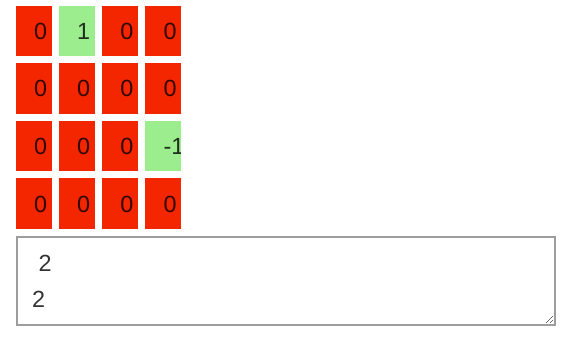
  • Jupyter+ipwidgets GUI for Nilpotents to Permutation Conjugacy Class Correspondence

    Jupyter+ipwidgets GUI for Nilpotents to Permutation Conjugacy Class Correspondence

    I was looking for a family of symplectic nilpotent matrices with prescribed associated permutation conjugacy classes. So I made a GUI in Jupyter+ipywidgets to go over matrices, and it actually worked.

    Here is the code the GUI:

    In [1]:
    from collections import Counter
import numpy as np
import ipywidgets as widgets
    In [2]:
    def get_k(A):
    """Get nullity sequence of A"""
    n = len(A)
    k = []
    for i in range(2 * n + 1):
        nullity = 2*n - np.linalg.matrix_rank(np.linalg.matrix_power(A, i))
        k.append(nullity)
        if nullity == 2 * n:
            break
    else:
        return None
    return np.array(list(filter(bool, np.diff(k))))

def k_to_perm(k):
    """Convert nullity sequence to permutation conjugacy class by taking dual and fancy python"""
    if k is None:
        return None
    perm = Counter()
    for i in range(1, max(k) + 1):
        perm += Counter({np.sum(k >= i)})
    return perm

def pretty_perm(p):
    """Return nice two-rowed representation of permutaion conjugacy class"""
    if p is None:
        return 'not nilpotent'
    top = ''
    bottom = ''
    for i in sorted(p.keys()):
        b = str(i)
        t = str(p[i])
        bottom += b + '  '
        top += (' ' * len(b)) + t + ' '
    return '%s\n%s' % (top, bottom)

def favorite_symplectic(n):
    w = np.zeros((n, n), np.int64)
    for i in range(n//2):
        w[i, n - i - 1] = 1
    for i in range(n//2, n):
        w[i,  n - i - 1] = -1
    return w

def favorite_orthogonal(n):
    w = np.zeros((n, n), np.int64)
    for i in range(n):
        w[i, n - i - 1] = 1
    return w

def show_grid(n, preserve=None):
    """Show nxn grid of buttons and a textarea for permutation conjugacy class"""
    if preserve is not None:
        if preserve == 'symplectic':
            preserve = favorite_symplectic(n)
        elif preserve == 'orthogonal':
            preserve = favorite_orthogonal(n)
        w_inv = np.linalg.inv(preserve)
        
    A = np.zeros((n, n), np.int64)
    bs = []
    txt = widgets.Textarea()
    
    for i in range(n):
        row = []
        for j in range(n):
            w = widgets.Button(description='0', layout=widgets.Layout(width='5px'))
            w.style.button_color = 'red'
            def foo(b, i=i, j=j):
                if b.description == '0':
                    v, c = 1, 'lightgreen'
                else:
                    v, c = 0, 'red'
                    
                A[i, j] = v
                b.description = str(v)
                b.style.button_color = c
                
                if preserve is not None:
                    M = np.zeros((n, n), np.int64)
                    M[i, j] = 1
                    M = -np.dot(np.dot(w_inv, M.T), preserve)
                    (i2,), (j2,) = np.where(M)
                    if (i, j) != (i2, j2):
                        A[i2, j2] = int(M[i2, j2] * v)
                        bs[i2][j2].description = str(A[i2, j2])
                        bs[i2][j2].style.button_color = c
                    
                txt.value = pretty_perm(k_to_perm(get_k(A)))
            w.on_click(foo)
            row.append(w)
        bs.append(row)

    display(widgets.VBox([widgets.HBox(row) for row in bs] + [txt]))
    In [3]:
    show_grid(4, 'orthogonal')

  • Counting Symplectic Matrices Satisfying Something

    While working on my thesis, I wanted to bound the dimension of a Jacquet module of a uniform character (i.e. a combination of Deligne-Lusztig characters) using an idea of Gelfand, appearing in ‘Representations of the full linear group over finite fields’ (1970). In modern terms, Gelfand shows that the cuspidal characters of $latex G=GL_n(\mathbb{F}_q)$ are generic/regular/have a Whittaker model.

    For a cuspidal representation $latex \tau$, and $latex \psi\in \hat{\mathbb{F}_q}$, a non-trivial additive character, Gelfand shows that (1): $latex (\textup{res}_U^G\ \tau,\psi)_U$ is a rational function of $latex q$ of degree $latex 0$, and (2): it equals $latex 1$ for all large enough $latex q$. Hence it is always $latex 1$.

    The first property is proved by a rather explicit computation. Gelfand shows that the number of upper triangular unipotent matrices in a given conjugacy class is a polynomial in $latex q$, and computes its degree. This is enough, since the character values of a cuspidal character at unipotent elements was already known, due to Green (I think). The second property essentially follows from the first and a multiplicity one result.

    I wanted to do the same with a representation of $latex Sp_{2n}(\mathbb{F}_q)$: show that the dimension of the Jacquet module with respect to some unipotent subgroup was a polynomial and that I can compute its degree. Specifically, I needed to compute the number of matrices such that

    $latex u=\begin{pmatrix}
    u’&M&Z \\
    &I_{2\ell}&M’ \\
    & &u’^*
    \end{pmatrix}\in Sp_{2m}(\mathbb{F}_q),$
    $latex \textup{rank}(u-1)=k,$
    $latex u’_{1,2}+u’_{2,3}+…+u’_{m-\ell,m-\ell+1}=c$

    for any positive integers $latex m, k, \ell$, and $latex c\in\mathbb{F}_q$. (The symplectic form is defined in the linked file below.)

    So I did. I knew that I didn’t have a formula for the values of my character at unipotent elements, but I knew that the values are polynomials, and I thought I knew their degrees. This would be enough to prove what I needed. But I was wrong. I did not know the degrees of the polynomials. I couldn’t find a way to compute them without doing some heavy lifting, like in Lusztig’s ‘On the Green Polynomials of Classical Groups’ (1976). Essentially, I was missing the following result: degrees of values at unipotent elements of “small” representations are smaller than degress of values from cuspidal representations. Small here means a semisimple representation that is not also regular. I still don’t know if this is true or not.

    But then I found a different way to bound the dimension of my Jacquet module: compute the character’s wave front set and use Lusztig’s results from ‘A unipotent support for irreducible representations’ (1992).

    Back to counting matrices. I use the same ideas from Gelfand’s paper, only extending the amount of variables I need to keep track of (not just rank). If you’re interested, here it is:

    http://www.math.tau.ac.il/~drorspei/Unipotent Symplectic Matrices Satisfying Something.pdf